A. HIPERBOLA
Hiperbola adalah tempat kedudukan titik-titik yang selisih jaraknya
terhadap dua titik tertentu selalu tetap.
Kedua titik tertentu itu dinamakan fokus.
Kedua titik tertentu itu dinamakan fokus.
Terdapat dua macam bentuk hiperbola,
yakni1. hiperbola horizontal
2. hiperbola vertical.
Secara lebih rinci akan dijelaskan menjadi empat bagian. (Rangkuman rumus berada paling bawah sendiri)
1. Hiperbola Horizontal dengan Pusat O(0, 0)
Bentuk Umum:
Unsur-unsurnya :
Koordinat titik puncaknya di A1(a, 0), A2(–a, 0)
Sumbu utama sumbu-X dan sumbu sekawan sumbu-Y
Titik fokus di F1(c, 0) dan F2(–c, 0) dimana c2 = a2 + b2
Nilai eksentrisitasnya
Persamaan garis amsistot dirumuskan:
Panjang Latus rectum:
2. Hiperbola Vertikal dengan Pusat O(0, 0)
Bentuk
umum :
Unsur-unsurnya:
Koordinat titik puncaknya di B1(0, b), dan B2(0, –b)
Sumbu utama sumbu-Y dan sumbu sekawan sumbu-X
Titik fokus di F1(0, c) dan F2(0, –c) dimana c2 = b2 + a2
Nilai eksentrisitasnya
Koordinat titik puncaknya di B1(0, b), dan B2(0, –b)
Sumbu utama sumbu-Y dan sumbu sekawan sumbu-X
Titik fokus di F1(0, c) dan F2(0, –c) dimana c2 = b2 + a2
Nilai eksentrisitasnya
Persamaan
garis amsistot dirumuskan:
Panjang
Latus rectum:
3. Hiperbola Horizontal dengan Pusat M(p, q)
Bentuk Umum:
Bentuk Umum:
Unsur-unsurnya
:
Koordinat titik puncaknya di A1(a + p, q), A2(–a + p, q)
Sumbu utama adalah y = q dan sumbu sekawan adalah x = p
Titik fokus di F1(c + p, q) dan F2(–c + p, q) dimana c2 = a2 + b2
Nilai eksentrisitasnya
Koordinat titik puncaknya di A1(a + p, q), A2(–a + p, q)
Sumbu utama adalah y = q dan sumbu sekawan adalah x = p
Titik fokus di F1(c + p, q) dan F2(–c + p, q) dimana c2 = a2 + b2
Nilai eksentrisitasnya
4. Hiperbola Vertikal dengan Pusat M(p, q)
Bentuk Umum:
Koordinat titik puncaknya di B1(p, b + q), dan B2(p, –b + q)
Sumbu utama adalah x = p dan sumbu sekawan adalah y = q
Titik fokus di F1(p, c + q) dan F2(p, –c + q) dimana c2 = b2 + a2
Nilai eksentrisitasnya
Panjang
Latus rectum:
B. HIPERBOLOID
Grafik dengan persamaan
adalah hiperboloid satu daun dengan sumbu mayor sumbu z.
Grafik dengan persamaan
adalah hiperboloid dua daun dengan sumbu
mayor sumbu z.
Grafik dengan persamaan
adalah sebuah hiperbolic paraboloid.
Grafik dengan persamaan
adalah kerucut dengan sumbu mayor adalah
sumbu z.
Persamaan
hiperboloida
Bentuk umum
persamaan ellipsoida adalah Ax2 + By2 + Cz2 +Gx + Hy + Iz + J = 0, dengan sekurang-kurangnya satu
dari hasil perkalian dua koefisien x2, y2, z2 adalah bilangan negatif.
"SEMOGA BERMANFAAT"






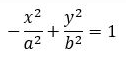




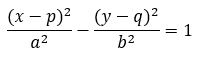













Tidak ada komentar:
Posting Komentar