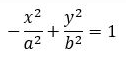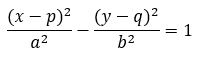Laporan UAS Praktikum Analitik
https://docs.google.com/document/d/1h8tL4tHsG8Bt4flCjE7qhwGvJFvX4aRrvqNduR-j1PU/edit?usp=sharing

File Geogebra
(File Geogebra soal 1)
  https://drive.google.com/open?id=1nO-WhAhLO68ebZWOWFC7nnBdz9hFzUUl
(File Geogebra Elipsoida)
https://drive.google.com/open?id=1ByMJiiXZO3KnbOsw2J9iQviuvNVOfmEc
(File Geogebra Bola)
https://drive.google.com/open?id=1gDx4MLMaML_W94FPw3wuksQQSeNGtUKT

Hiperbola dan Hiperboloid

A. HIPERBOLA

Hiperbola adalah tempat kedudukan titik-titik yang selisih jaraknya terhadap dua titik tertentu selalu tetap.
Kedua titik tertentu itu dinamakan fokus.

Terdapat dua macam bentuk hiperbola,

yakni
1. hiperbola horizontal
2. hiperbola vertical.

Secara lebih rinci akan dijelaskan menjadi empat bagian. (Rangkuman rumus berada paling bawah sendiri)

1. Hiperbola Horizontal dengan Pusat O(0, 0)

Bentuk Umum:

Unsur-unsurnya :
Koordinat titik puncaknya di A1(a, 0), A2(–a, 0)
Sumbu utama sumbu-X dan sumbu sekawan sumbu-Y
Titik fokus di F1(c, 0) dan F2(–c, 0) dimana c² =  a² + b²
Nilai eksentrisitasnya

Persamaan garis amsistot dirumuskan:

Panjang Latus rectum:

2. Hiperbola Vertikal dengan Pusat O(0, 0)

Bentuk umum :

Unsur-unsurnya:
Koordinat titik puncaknya di B1(0, b), dan B2(0, –b)
Sumbu utama sumbu-Y dan sumbu sekawan sumbu-X
Titik fokus di F1(0, c) dan F2(0, –c) dimana c² =  b² + a²
Nilai eksentrisitasnya

Persamaan garis amsistot dirumuskan:

Panjang Latus rectum:

3. Hiperbola Horizontal dengan Pusat M(p, q)

Bentuk Umum:

Unsur-unsurnya :
Koordinat titik puncaknya di A1(a + p, q), A2(–a + p, q)
Sumbu utama adalah y = q dan sumbu sekawan adalah x = p
Titik fokus di F1(c + p, q) dan F2(–c + p, q) dimana c² =  a² + b²
Nilai eksentrisitasnya

Persamaan garis asimstot dirumuskan:

Panjang Latus rectum:

4. Hiperbola Vertikal dengan Pusat M(p, q)

Bentuk Umum:

Unsur-unsurnya:
Koordinat titik puncaknya di  B1(p, b + q), dan B2(p, –b + q)
Sumbu utama adalah x = p dan sumbu sekawan adalah y = q
Titik fokus di F1(p, c + q) dan F2(p, –c + q) dimana c² =  b² + a²
Nilai eksentrisitasnya

Persamaan garis asimstot dirumuskan:

Panjang Latus rectum:

B. HIPERBOLOID

Grafik dengan persamaan  

 adalah hiperboloid satu daun dengan sumbu mayor sumbu z.

Grafik dengan persamaan 

  adalah hiperboloid dua daun dengan sumbu mayor sumbu z.

Grafik dengan persamaan 

 adalah sebuah hiperbolic paraboloid.

Grafik dengan persamaan 

 adalah kerucut dengan sumbu mayor adalah sumbu z.

Persamaan hiperboloida

Bentuk umum persamaan ellipsoida adalah Ax² +  By² + Cz² +Gx + Hy + Iz + J = 0, dengan sekurang-kurangnya satu dari  hasil perkalian dua koefisien x², y², z² adalah bilangan negatif.

"SEMOGA BERMANFAAT"

Analisis Video Parabola dan Paraboloid

PARABOLA

Analisis:

Pada parabola ada yang terbuka keatas dan ada yang terbuka kebawah.

Parabola memiliki sumbu simetri yang membagi jarak titik pada parabola ketitik fokus itu sama.

PARABOLOID

Analisis :

Paraboloid yang mengelilingi sumbu Z persamaannya : x²/a² + y²/b² = z/c

Ketika z =0 maka persamaannya menjadi : x²/a² + y²/b² =0 dan bidang z ada di z=0

Dan ketika z= 4 maka persamaannya menjadi : x²/a² + y²/b² =4/c dan bidang z ada di  z=4

"SEMOGA BERMANFAAT"

Pengertian dan Unsur-Unsur Ellips

• PENGERTIAN ELLIPS

Ellips adalah himpunan semua titik yang jumlah jaraknya terhadap dua titik tertentu tetap besarnya. Dua titik tertentu itu disebut fokus atau titik api (F₁ dan F₂), jarak (F₁dan F₂) adalah 2c, dan jumlah jarak tetap 2a (a > 0)

• UNSUR-UNSUR ELLIPS

Keterangan:

v  O : titik pusat ellips O (0,0)

v  A₁ dan A₂ : Titik puncak sumbu mayor

v  B₁ dan B₂ : Titik puncak sumbu minor

v  A₁O=OA₂=a

v  B₁O=OB₂=b

v  F₁ dan F₂ : Titik fokus, dengan a² = b² + c²

v  A₁A₂ : Sumbu mayor / sumbu panjang = 2a

v  B₁B₂ : Sumbu Minor / Sumbu Pendek = 2b

v  d₁ dan d₂ : Direktriks

v  TU : Lactus Rectum (LR): 2b²/a

v  Eksentrisitas : e=c/a

Eksentrisitas (e) merupakan ukuran kelonjongan ellips dan didefinisikan sebagai :

0<e<1 : ellips

e = 0 : lingkaran

e = 1 : garis lurus / parabola 

" SEMOGA BERMANFAAT"

Irisan Kerucut

Dalam geometri, kerucut adalah sebuah limas istimewa yang beralas lingkaran. Kerucut memiliki 2 sisi dan 1 rusuk.

Sisi tegak kerucut tidak berupa segitiga tapi berupa bidang miring yang disebut selimut kerucut.

Jika kerucut diiris dari berbagai arah, hasil irisannya akan membentuk beberapa bangun.Bagian kerucut yang dipotong suatu bidang, hasil potongan tersebut akan membentuk sebuah bangun. Jika dipotong secara mendatar, hasil potongan kerucut berupa lingkaran. Kerucut yang dipotong dengan arah sudut tertentu akan membentuk elips atau parabola. Potongan secara tegak menghasilkan bangun hiperbola.

Berikut ini adalah gambar kerucut yang dipotong dari beberapa arah sehingga menghasilkan lingkaran, elips, parabola, dan hiperbola.

"SEMOGA BERMANFAAT"

P5_K3_4A (Manual)

Kelompok 3 :

1. Dwi Lestari (A1C017015)

2. Rezki Ainun Sari (A1C017033)

3. Darna Dwi Yuliani (A1C017049)